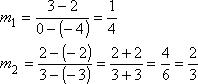Let's take a look at the straight line y = ( 2/3 ) x – 4. Its graph looks like this:
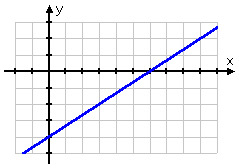
Pick two x's and solve for each corresponding y: If, say, x = 3, then y = ( 2/3 )(3) – 4 = 2 – 4 = –2. If, say, x = 9, then y = ( 2/3 )(9) – 4 = 6 – 4 = 2. (By the way, I picked the x-values to be multiples of three because of the fraction. It's not a rule that you have to do that, but it's a helpful technique.) So the two points (3, –2) and (9, 2) are on the line y = ( 2/3 )x – 4.
To find the slope, you use the following formula:
The subscripts merely indicate that you have a "first" point (whose coordinates are subscripted with a "1") and a "second" point (whose coordinates are subscripted with a "2"); that is, the subscripts indicate nothing more than the fact that you have two points to work with. It is entirely up to you which point you label as "first" and which you label as "second". For computing slopes with the slope formula, the important thing is that you subtract the x's and y's in the same order. For our two points, if we choose (3, –2) to be the "first" point, then we get the following:
|
|
|
|
|
|
Technically, the equivalence of the two slope formulas above can be proved by noting that:
- y1
– y2
= –y2
+ y1 = –(y2
– y1)
x1 – x2 = –x2 + x1 = –(x2 – x1)
Let's find the slope of another line equation:
- Find the slope of y = –2x + 3.
|
Graphing the line,
it looks like this: |
|
 |
Scroll back up this page and look at those equations and their graphs. For the first equation, y
= ( 2/3 )x – 4, the slope was m = 2/3. And the line, as you moved from left to right along the x-axis, was heading up toward the top of the drawing; technically, the line was "increasing". For the second line, y = –2x + 3, the slope was m = –2. And the line, as you moved from left to right along the x-axis, was heading down toward the bottom of the drawing; technically, the line was "decreasing". This relationship is always true: Increasing lines have positive slopes, and decreasing lines have negative slopes. Always!
This fact can help you check your calculations: if you calculate a slope as being negative, but you can see from the graph that the line is increasing (so the slope must be positive), you know you need to re-do your calculations. Being aware of this connection can save you points on a test because it will enable you to check your work before you hand it in.
Increasing lines
have positive slopes; decreasing lines have negative slopes. With
this in mind, consider the following horizontal line:
|
|
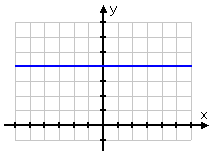 |
|
Now consider the vertical line x = 4: Is the vertical line going up on one end? Well, kind of. Is the vertical line going down on the other end? Well, kind of. Is there any number that is both positive and negative? Nope. |
|
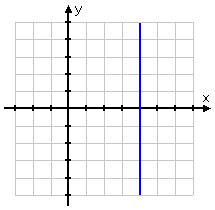 |
This relationship is always true: a vertical line will have no slope, and "the slope is undefined" means that the line is vertical. (By the way, all vertical lines are of the form "x = some number", and "x = some number" means the line is vertical. Any time your line involves an undefined slope, the line is vertical, and any time the line is vertical, you'll end up dividing by zero if you try to compute the slope.)
Warning: It is very common to confuse these two lines and their slopes, but they are very different. Just as "horizontal" is not at all the same as "vertical", so also "zero slope" is not at all the same as "no slope". The number "zero" exists, so horizontal lines do indeed have a slope. But vertical lines don't have any slope; "slope" just doesn't have any meaning for vertical lines. It is very common for tests to contain questions regarding horizontals and verticals. Don't mix them up!
Parallel lines and their slopes are easy. Since slope is a measure of the angle of a line from the horizontal, and since parallel lines must have the same angle, then parallel lines have the same slope — and lines with the same slope are parallel.
|
|
|
|
|
|
In your homework, you will probably be given some pairs of points, and be asked to state whether the lines through the pairs of points are "parallel, perpendicular, or neither". To answer the question, you'll have to calculate the slopes and compare them. Here's how that works:
- One line passes through the points (–1, –2) and (1, 2); another line passes through the points (–2, 0) and (0, 4). Are these lines parallel, perpendicular, or neither?
- To answer this question, I'll find the
slopes.
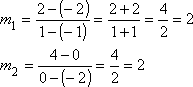
- One line passes through the points (0, –4) and (–1, –7); another line passes through the points (3, 0) and (–3, 2). Are these lines parallel, perpendicular, or neither?
- I'll find the values of the slopes.
Copyright © Elizabeth Stapel
2000-2011 All Rights Reserved
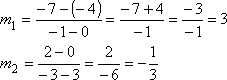
- One line passes through the points (–4, 2) and (0, 3); another line passes through the points (–3, –2) and (3, 2). Are these lines parallel, perpendicular, or neither?
- I'll find the slopes.