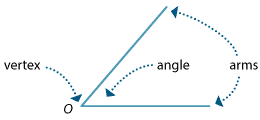
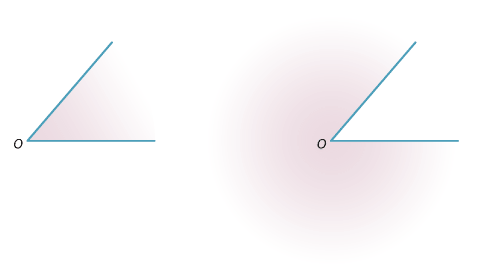When two lines meet at a point, they make an angle. The two lines are called the arms of the angle and the point is called the vertex.
Two angles are created. One angle falls inside the arms, and the other angle falls outside them.
To measure the angle we see how much one of the lines must be turned through the shaded area to get to the other line.
An understanding of angles forms the basis of much of the geometry you will meet in upper primary and in secondary school. Geometry, including angles, has been used throughout history. The Egyptians must have had a very good knowledge of angles to construct the pyramids so perfectly.
Two angles are created. One angle falls inside the arms, and the other angle falls outside them.
To measure the angle we see how much one of the lines must be turned through the shaded area to get to the other line.
An understanding of angles forms the basis of much of the geometry you will meet in upper primary and in secondary school. Geometry, including angles, has been used throughout history. The Egyptians must have had a very good knowledge of angles to construct the pyramids so perfectly.