Special Parallelograms
A parallelogram may be equiangular (rectangle), equilateral (rhombus) or both equiangular and equilateral. An example of a special parallelogram that is both equiangular and equilateral is our friend the square.Rectangle
A rectangle is a parallelogram with 4 right angles. A rectangle has the following rules:(1) All the rules of a parallelogram.
(2) Four right angles. Remember that a right angle measures 90 degrees.
(3) Diagonals which are congruent (they have the same length).
The picture of rectangle ABCD below shows all three rules listed above.

Sample:
In rectangle ABCD below, diagonals AC and BD intersect at point R. If AR = 2x - 6 and CR = x + 10, find BD.

Since the diagonals of a rectangle bisect each other, we can say that
AR = CR.
We equate the values of AR and CR and solve for x.
2x - 6 = x + 10
2x - x = 10 + 6
x = 16
Use either of the given equations to determine that each segment equals 26. Since they are all equal, BD = 26.
Rhombus
A rhombus is a parallelogram with 4 congruent or equal sides. A rhombus has the following rules:(1) All the rules of a parallelogram.
(2) Four sides that have the same length.
(3) Diagonals that intersect at right angles.
(4) Diagonals that bisect opposite pairs of angles.

Sample:
Given that ABCD is a rhombus and the measure of angle D = 60 degrees.
Find the measure of angles A and B.

Solution:
Triangle ABC is isosceles since line segment AB is congruent to line segment BC. Then we can say that the base angles of triangle ABC must be congruent or equal. Since we know the diagonal bisects the angles A and C, we must have two congruent triangles here. If so, then the measure of angle D = the measure of angle B = 60 degrees.

In triangle AEB, angle AEB is a right triangle because the diagonals of a rhombus are perpendicular to each other. Since the sum of the degree measures of the angles of a triangle is 180 degrees, we can say that the measure of angle A must be 30 degrees. How do we get 30?

Measure of angle A = 180 - 90 degrees - 60 degrees
Measure of angle A = 30 degrees
Square
A square is a parallelogram with 4 right angles and 4 sides that have the same length. A square has all the rules of a rectangle and a rhombus as shown in square ABCD below.
Sample:
In square ABCD, AB = x + 4. What is the perimeter of square ABCD?
Solution:
A square has the same length on all 4 sides.
We can use the formula P = side times 4, or P = 4s, where P = perimeter and s = side of square.
P = 4s
P = 4(x + 4)....We apply the distributive rule here and get
P = 4x + 16
Our perimeter is 4x + 16.



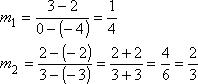





![\left [ (p \to q)\wedge p \right ] \to q](http://www.mathplanet.com/images/math/codecogs_cd305aa.png)
![\left [ (p \to q)\wedge (q \to r ) \right ] \to (p \to r)](http://www.mathplanet.com/images/math/codecogs_13db2bf9.png)